Page 6 - Demo
P. 6
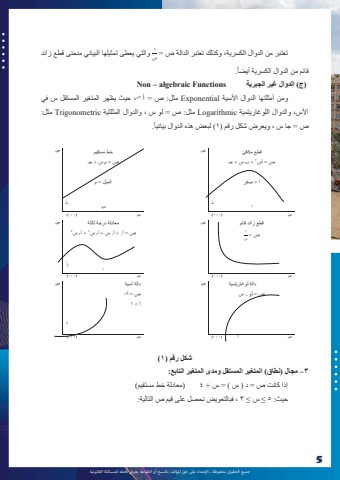
%u062c%u0645%u064a%u0639 %u0627%u0644%u062d%u0642%u0648%u0642 %u0645%u062d%u0641%u0648%u0638%u0629 %u0640 %u0627%u0625%u0644%u0639%u062a%u062f%u0627%u0621 %u0639%u0649%u0644 %u062d%u0642 %u0627%u0645%u0644%u0624%u0644%u0641 %u0628%u0627%u0644%u0646%u0633%u062e %u0623%u0648 %u0627%u0644%u0637%u0628%u0627%u0639%u0629 %u064a%u0639%u0631%u0636 %u0641%u0627%u0639%u0644%u0647 %u0644%u0644%u0645%u0633%u0627%u0626%u0644%u0629 %u0627%u0644%u0642%u0627%u0646%u0648%u0646%u064a%u0629531 %u062a%u0639%u062a%u0628%u0631 %u0645%u0646 %u0627%u0644%u062f%u0648%u0627%u0644 %u0627%u0644%u0643%u0633%u0631%u064a%u0629%u060c %u0648%u0643%u0630%u0644%u0643 %u062a%u0639%u062a%u0628%u0631 %u0627%u0644%u062f%u0627%u0644%u0629 %u0635 = %u0648%u0627%u0644%u062a%u064a %u064a%u0639%u0637%u0649 %u062a%u0645%u062b%u064a%u0644%u0647%u0627 %u0627%u0644%u0628%u064a%u0627%u0646%u064a %u0645%u0646%u062d%u0646%u0649 %u0642%u0637%u0639 %u0632%u0627%u0626%u062f %u0633%u064b.%u0642%u0627%u0626%u0645 %u0645%u0646 %u0627%u0644%u062f%u0648%u0627%u0644 %u0627%u0644%u0643%u0633%u0631%u064a%u0629 %u0623%u064a%u0636%u0627)%u062c( %u0627%u0644%u062f%u0648%u0627%u0644 %u063a%u064a%u0631 %u0627%u0644%u062c%u0628%u0631%u064a%u0629 Functions algebraic %u2013 Non%u060c %u062d%u064a%u062b %u064a%u0638%u0647%u0631 %u0627%u0644%u0645%u062a%u063a%u064a%u0631 %u0627%u0644%u0645%u0633%u062a%u0642%u0644 %u0633 %u0641%u064a %u0633 %u0648%u0645%u0646 %u0623%u0645%u062b%u0644%u062a%u0647%u0627 %u0627%u0644%u062f%u0648%u0627%u0644 %u0627%u0623%u0644%u0633%u064a%u0629 Exponential %u0645%u062b%u0644: %u0635 = %u0623%u0627%u0623%u0644%u0633%u060c %u0648%u0627%u0644%u062f%u0648%u0627%u0644 %u0627%u0644%u0644%u0648%u063a%u0627%u0631%u064a%u062a%u0645%u064a%u0629 Logarithmic %u0645%u062b%u0644: %u0635 = %u0644%u0648 %u0633 %u060c %u0648%u0627%u0644%u062f%u0648%u0627%u0644 %u0627%u0644%u0645%u062b%u0644%u062b%u064a%u0629 Trigonometric %u0645%u062b%u0644: %u064b.%u0635 = %u062c%u0627 %u0633 %u060c %u0648%u064a%u0639%u0631%u0636 %u0634%u0643%u0644 %u0631%u0642%u0645 )1 )%u0644%u0628%u0639%u0636 %u0647%u0630%u0647 %u0627%u0644%u062f%u0648%u0627%u0644 %u0628%u064a%u0627%u0646%u064a%u0627%u0642%u0637%u0639 %u0645%u0643%u0627%u0641%u0626 2 + %u0628 %u0633 + %u062c%u0640 %u0635 = %u0623%u0633%u0623 > %u0635%u0641%u0631%u0635 %u062e%u0637 %u0645%u0633%u062a%u0642%u064a%u0645 %u0635 = %u0645 %u0633 + %u062c%u0640 %u0627%u0644%u0645%u064a%u0644 = %u0645 %u0635%u2193%u062c%u0640%u2191%u2193%u062c%u0640%u0633%u2191%u0633 )0 %u060c 0 )%u0633 )0 %u060c 0)%u0642%u0637%u0639 %u0632%u0627%u0626%u062f %u0642%u0627%u0626%u0645 %u0635 = 1%u0633%u0635 %u0645%u0639%u0627%u062f%u0644%u0629 %u062f%u0631%u062c%u0629 %u062b%u0627%u0644%u062b%u0629 2 + %u06233 %u0633 3%u0635 = %u06230 + %u06231 %u0633 + %u06232 %u0633 %u0635%u2193%u2191 %u06230%u0633 )0 %u060c 0 )%u0633 )0 %u060c 0) %u062f%u0627%u0644%u0629 %u0644%u0648%u063a%u0627%u0631%u064a%u062a%u0645%u064a%u0629 %u0635 = %u0644%u064810 %u0633 %u0635 %u062f%u0627%u0644%u0629 %u0623%u0633%u064a%u0629 %u0635 = %u0623%u0633 %u0623 < 1%u06351%u0633 1( 0 %u060c 0 )%u0633 )0 %u060c 0)%u0634%u0643%u0644 %u0631%u0642%u0645 ) 1 )3 %u2013%u0645%u062c%u0627%u0644 )%u0646%u0637%u0627%u0642( %u0627%u0644%u0645%u062a%u063a%u064a%u0631 %u0627%u0644%u0645%u0633%u062a%u0642%u0644 %u0648%u0645%u062f%u0649 %u0627%u0644%u0645%u062a%u063a%u064a%u0631 %u0627%u0644%u062a%u0627%u0628%u0639:%u0625%u0630%u0627 %u0643%u0627%u0646%u062a %u0635 = %u062f ) %u0633 ( = %u0633 + 4( %u0645%u0639%u0627%u062f%u0644%u0629 %u062e%u0637 %u0645%u0633%u062a%u0642%u064a%u0645( %u062d%u064a%u062b: 5 %u2265 %u0633 %u2264 3 %u060c %u0641%u0628%u0627%u0644%u062a%u0639%u0648%u064a%u0636 %u0646%u062d%u0635%u0644 %u0639%u0644%u0649 %u0642%u064a%u0645 %u0635 %u0627%u0644%u062a%u0627%u0644%u064a%u0629: